피어슨 상관계수와 공분산
피어슨 상관계수
-1 부터 1 사이 값을 가진다. 상관계수가 1에 가까울수록 두 변수는 강한 양의 상관관계가 있고, 반대로 상관계수가 -1에 가까울 수록 강한 음의 상관관계가 있다고 볼 수 있다.
피어슨 상관관계 값을 계산하려면 두 변수의 '공분산(covariance)'이라는 값을 구해서, 공분산을 각 변수의 표준 편차의 곱으로 나눠 줘야 한다. 예를 들어 X라는 변수와 Y라는 변수가 있다고 하면, X와 Y의 공분산 값을 X의 표준 편차와 Y의 표준 편차의 곱으로 나눠 주는 것이다. 공식을 보자면,



이렇게 사용한다.
공분산이란?
공분산은 두 변수 간의 관계의 방향성과 강도를 측정할 때 사용할 수 있는 통계 값이다. X와 Y의 공분산은 아래와 같은 수식을 통해 계산 할 수 있다.
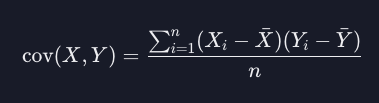
즉, 공분산을 구하려면 각 값과 해당 변수의 평균값 간의 편차를 곱하여 모두 더한 뒤, 데이터의 총 개수로 나눠 주면 된다.
하나의 변수가 증가할 때 다른 변수도 증가하는 경향이 있다면 공분산 값은 양수가 되고, 반대로 하나의 변수가 증가할 때 다른 변수는 감소한다면 공분산 값은 음수가 된다. 얼핏 보면 개념 자체는 상관계수와 거의 비슷해 보이지만, 공분산 값의 크기는 변수의 단위에 큰 영향을 받는다는 한계가 있다. 예를 들면 무게는 그램, 킬로그램, 톤 등 다양한 단위를 사용해서 표한할 수 있고, 길이는 센티미터, 미터, 킬로미터 등으로 표현할 수 있다. 간단히 말하면, 이 단위에 따라 공분산 값의 범위가 크게 달라진다는 뜻이다. 따라서 공분산 값이 크게 나왔을 때, 정말로 상관관계가 커서 그런 건지, 단지 변수의 단위 때문에 숫자가 커서 그런 건지 판단할 수가 없다.
그런데 피어슨 상관계수는 이런 공분산을 각 변수의 표준 편차의 곱으로 나눠서, -1에서 1사이의 값을 가지도록 만든다. 즉, 변수의 단위에 관계없이 상관관계의 방향과 강도를 좀 더 객관적으로 비교할 수 있는 것이다.
공분산과 피어슨 상관계수는 변수 간의 상관관계를 표현할 때 유용하게 활용되는 통계 값이다.